Computer Arithmetic and Hardware Implementation |
Computer arithmetic deals with mathematical functions that are suitable for hardware implementation.It is fundamental to the designs of processor IU (integer unit) and FPU (floating point unit).
The basic operations computer arithmetic deals with include add, subtract, multiplication, division, and square root. Square root algorithm and its hardware implementation have been getting more attentions recent years in the designs of general-purpose processors, CG (computer graphics), and embedded CPUs.
Let's take an example to see how to calculate the square root of a decimal number by hand: Try to calculate the square root of 30,000,000,000.
_1__7__3__2__0__5_
1 / 3 00 00 00 00 00 (1 is the largest number such that 1 * 1 < 3)
1 -1 <--- 1 * 1 = 1
----------------------
27 2 00 <--- 1 + 1 = 2 (7 is the largest number such that 27 * 7 < 200)
7 -1 89 <--- 27 * 7 = 189
----------------------
343 11 00 <--- 27 + 7 = 34 (3 is the largest number such that 343 * 3 < 1100)
3 -10 29 <--- 343 * 3 = 1029
----------------------
3462 71 00 <--- 343 + 3 = 346 (2 is the largest number such that 3462 * 2 < 7100)
2 -69 24 <--- 3462 * 2 = 6924
----------------------
34640 1 76 00 <--- 3462 + 2 = 3464 (0 is the largest number such that 34640 * 0 < 17600)
0 -0 <--- 34640 * 0 = 0
----------------------
346405 1 76 00 00 <--- 34640 + 0 = 34640 (5 is the largest number such that 346405 * 5 < 1760000)
5 -1 73 20 25 <--- 346405 * 5 = 1732025
----------------------
2 79 75 <--- remainder
That is, the square root of 30,000,000,000 is 173,205 and the remainder is 27,975.
The reason why this algorithm works is explained below. We separated the decimal number into groups with 2 digits in each group, starting from the decimal point (in our example, the left-most group, 1, can be considered as 01). The largest value of a group is 99 = 10 * 9 + 9. We use AB to denote this number. That means AB = 10 * A + B. The square root of AB is denoted as a. Then we have a ≤ 9. Suppose we have calculated a and subtracted a2 from AB: R = AB - a2.
Now, consider ABCD - (ab)2. Because (ab)2 = (10 * a + b)2 = 100 * a2 + 20 * a * b + b2. Then
This procedure is repeated until all the groups are calculated. We have proposed a non-restoring (on remainder) square root algorithm for binary numbers. The following is a C version of the algorithm.
unsigned squart(D, r) // Non-Restoring square root
unsigned D; // D:32-bit unsigned integer to be square rooted
int *r; // Remainder
{
unsigned Q = 0; // Q:16-bit unsigned integer (root)
int R = 0; // R:17-bit integer (remainder)
int i;
for (i = 15; i >= 0; i--) { // for each root bit
if (R >= 0) { // remainder: non-negative
R = (R << 2) | ((D >> (i + i)) & 3); // new remainder
R = R - ((Q << 2) | 1); // R = R - Q01
} else { // remainder: negative
R = (R << 2) | ((D >> (i + i)) & 3); // new remainder
R = R + ((Q << 2) | 3); // R = R + Q11
}
if (R >= 0) Q = (Q << 1) | 1; // new Q bit 1
else Q = (Q << 1) | 0; // new Q bit 0
}
if (R < 0) R = R + ((Q << 1) | 1); // remainder adjusting
*r = R; // return remainder
return(Q); // return root
}
Here is an 8-bit example: D = 01111111 (127). We got Q = 1011 (11) and R = 0110 (6). That is, 127 = 112 + 6.
D = 01 11 11 11 R = 0 Q = 0000 R: non-negative
R = 01
- 01 (-Q01)
R = 00 11 Q = 0001 R: non-negative
- 01 01 (-Q01)
R = 11 10 11 Q = 0010 R: negative
+ 00 10 11 (+Q11)
R = 00 01 10 11 Q = 0101 R: non-negative
- 00 01 01 01 (-Q01)
R = 00 00 01 10 Q = 1011 R: non-negative
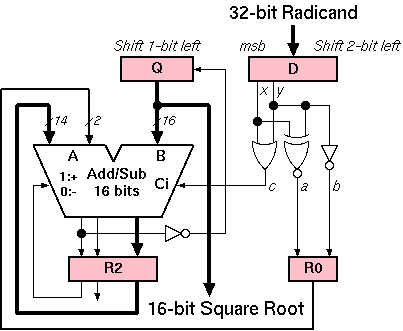
We have developed a VLSI (very large scale integration) implementation for the non-restoring square root algorithm. To my knowledge, this implementation is the simplest one in the world.

Our algorithm has the following features unlike other square root algorithms. First, the focus of the ``non-restoring'' is on the ``partial remainder'', not on ``each bit of the square root'', with each iteration. Second, it only requires one traditional adder/subtracter in each iteration, i.e., it does not require other hardware components, such as seed generators, multipliers, or even multiplexers. Third, it generates the correct resulting value even in the last bit position. Next, based on the resulting value of the last bit, a precise remainder can be obtained immediately without any correction or addition operation. And finally, it can be implemented at very fast clock rate because of the very simple operations at each iteration.
References
Computer Architecture/Organization and CPU Design |
Computer architecture is concerned with the structure and behavior of the various functional modules of computer and how they interact to provide the processing needs for the user. Computer organization is concerned with the way the hardware components are connected together to form a computer system. Computer design is concerned with the development of the hardware for the computer taking into consideration of a given set of specifications.
CPU (central processing unit) or processor is a key component in the computer design. The techniques used to design a CPU include pipelining, superscalar, multithreading, and multi-core (or chip multiprocessors).
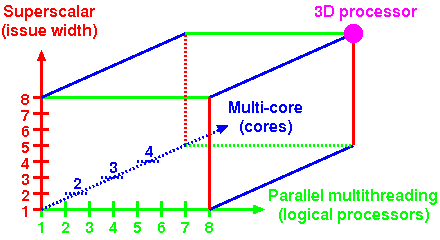
We have developed several models and prototypes in this field.
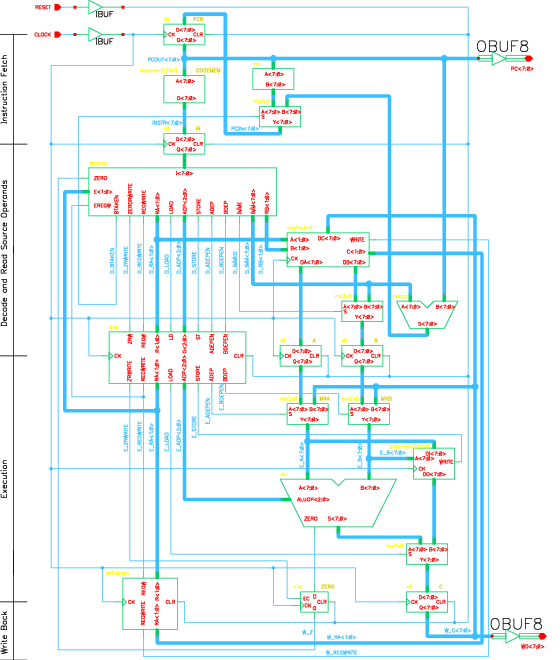
We have developed a RISC pipelined processor (Aizup) and implemented it on the Xilinx XC4006PC84 FPGA chip for the education purpose. The Aizup processor pipeline has four stages and deals with data dependency and control dependency. Some techniques for performance optimization, such as data forwarding, delay branch, and instruction reorganization, can be demonstrated in the design.
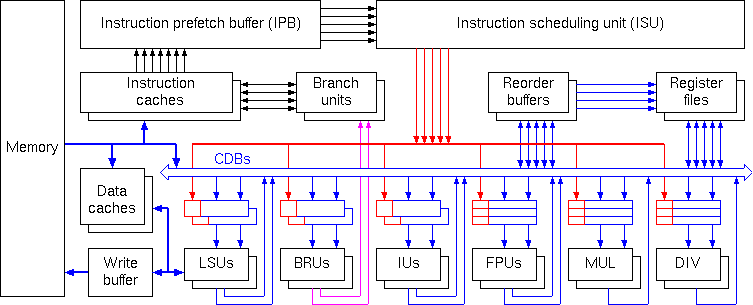
The multiple-threaded multiple-pipelined (or parallel multithreading) architecture can make multiple pipelines busy and hence can further improve the processor performance. Multiple thread slots dispatch instructions from multiple threads simultaneously. A thread slot is a hardware unit that is responsible for fetching and decoding instruction. Usually, the number of thread slots is less than the number of instruction threads. The instructions are executed in functional units.
We have developed a general-purpose parallel multithreading CPU and a Java Bytecode parallel multithreading CPU. The performance improvement is also evaluated through the trace-driven simulation.
References
Interconnection Networks and Fault-Tolerant Routing |
Interconnection networks are used both in parallel processing and in communication systems to exchange information. The popular topologies of interconnection networks include ring, mesh, torus, and hypercube, as shown as below.
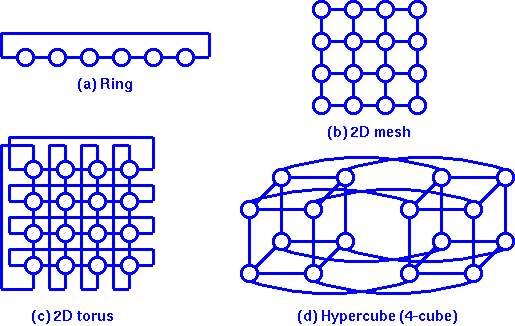
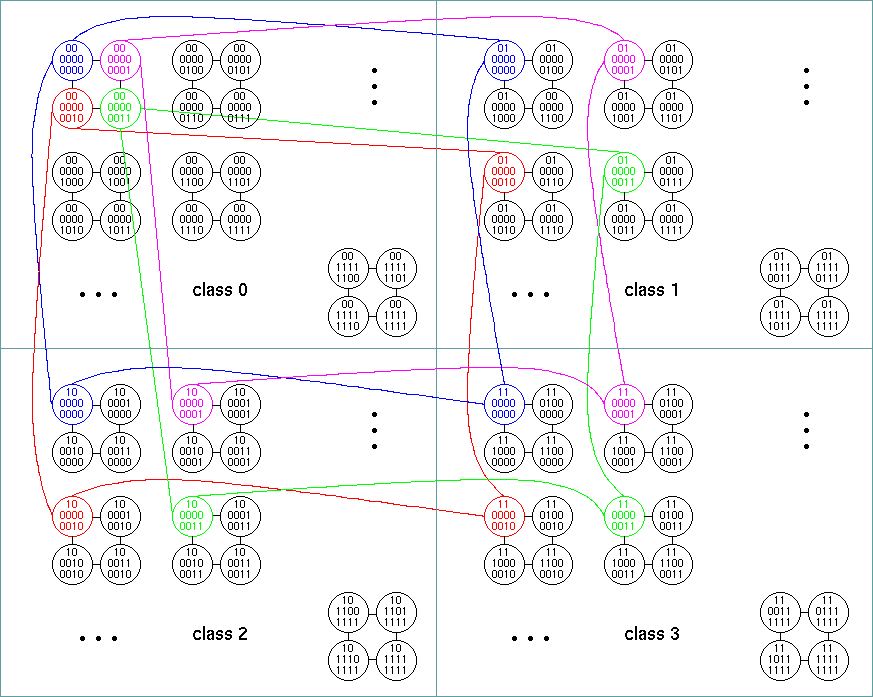
The hypercube has been widely used as the interconnection network for parallel computers. However, in hypercubes, the number of communication links for each node is a logarithmic function of the total number of nodes. Therefore, the hypercube is not a good candidate for an interconnection network for a very large parallel computer that might contain hundreds of thousands of nodes due to IC technology and port number limitations. We introduced a new interconnection network for very large parallel computers called metacube (MC). An MC network has a 2-level cube structure. An MC(k, m) network can connect 2m2k+k nodes with m+k links per node, where k is the dimension of the high-level cubes (classes) and m is the dimension of the low-level cubes (clusters). An MC network is a symmetric network with short diameter, easy and efficient routing and broadcasting similar to that of the hypercube. However, an MC network can connect millions of nodes with up to 6 links per node. An MC(2,3) with 5 links per node has 16,384 nodes and an MC(3,3) with 6 links per node has 134,217,728 nodes. We describe the MC network's structure, topological properties and routing and broadcasting algorithms.
The following figure shows a metacube with k=2 and m=2.
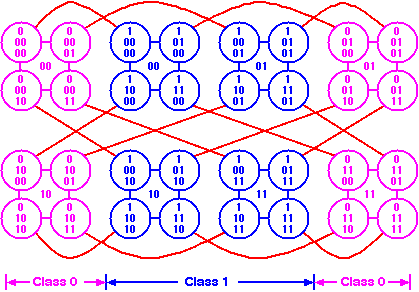
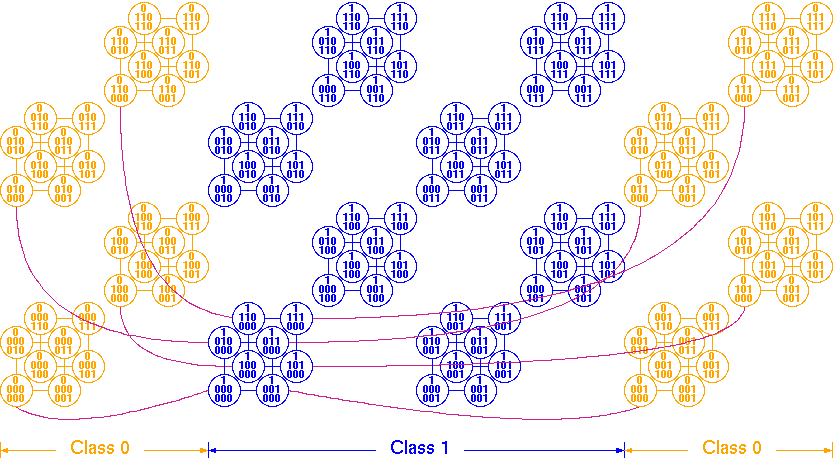
Let k=1 in metacube, we get dual-cube. The following figures show dual-cubes with m=2 and m=3, respectively.
Design of efficient routing algorithms for collective communications is the key issue in message-passing parallel computers or networks. Collective communications are required in load balancing, event synchronization, and data exchange. Based on the number of sending and receiving processors, these communications can be classified into one-to-many, one-to-all, many-to-many and all-to-all. The nature of the messages to be sent can be classified as personalized or non-personalized (multicast or broadcast). The all-to-all personalized communication (total exchange) is at the heart of numerical applications. We have presents efficient algorithms for collective communications in dual-cube.
Much effort has been devoted to introduce realistic definitions to measure the networks' ability to tolerate faults, and to develop routing algorithms under a large number of faults.
We proposed an efficient fault-tolerant routing algorithm for hypercube networks with a very large number of faulty nodes. The algorithm is distributed and local-information-based in the sense that each node in the network knows only its neighbors' status and no global information of the network is required by the algorithm. For any two given nonfaulty nodes in a hypercube network that may contain a large fraction of faulty nodes, the algorithm can find a fault-free path of nearly optimal length with very high probability. The algorithm uses the adaptive binomial-tree to select a suitable dimension to route a node. We perform empirical analysis of our algorithm through simulations under a uniform node failure distribution and a clustered node failure distribution. The experimental results show that the algorithm successfully finds a fault-free path of nearly optimal length with the probability larger than 90 percent in a hypercube network that may contain up to 50 percent faulty nodes.
References